シーソーによる論理素子

Created by Masashi Satoh | 11/21/2025

はじめに

リレーによる加算機の製作に入る前に、生徒たちに機械式の論理素子に触れさせます。その意図は以下のように整理できるでしょう。

• この実習により、私たちはコンピュータ＝電子的なマシンという誤ったイメージから離れることができます。
• コンピュータの原理は、その実装から独立していることを学びます。
• コンピュータが、物理現象などの観察から引き出された仕組みではなく、人間の思考を特定の物理現象に対応づけて模倣させていることを知ります。

装置に取り組む前に、以前、○×で考察した真理値表を01の表記に置き換える旨を生徒に説明します。なぜなら、これから作ろうとする装置では、ON/OFFを数値と見なして操作するのですから。

動作

NOT

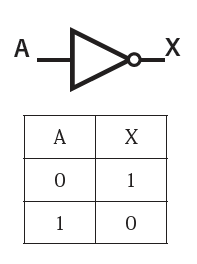
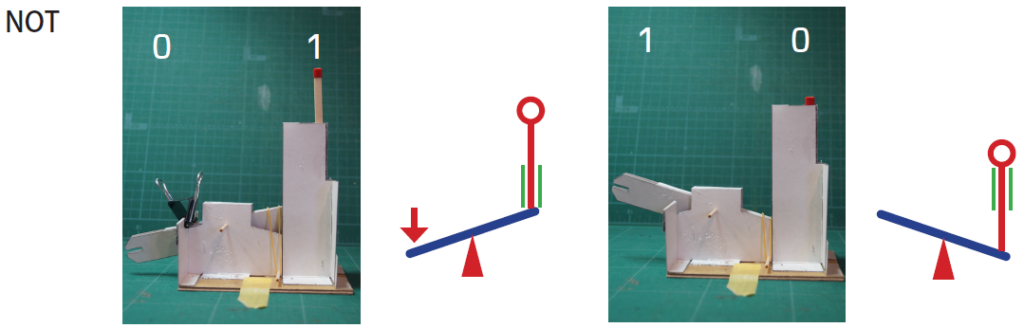
シーソーによるNOTの仕組みは極めて明快です。シーソー自体がNOTそのものだからです。

NOT回路は人数分用意し、生徒ひとりひとりが取り組めるようにします。

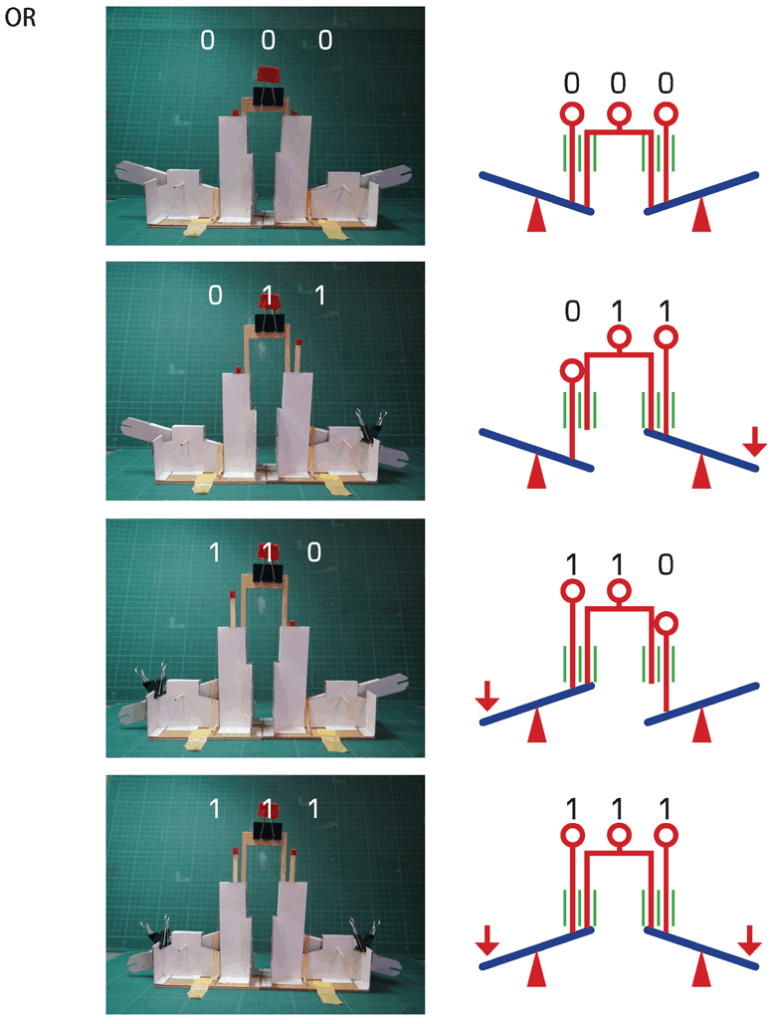
OR

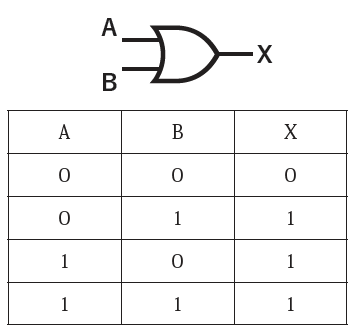
シーソーでORを作ることも比較的容易です。コの字のブリッジをふたつのシーソーに渡して、これを出力Xと見なせばよいのです。生徒たちをペアにして、2つのシーソーを用います。生徒たちに何も説明しなくても、ブリッジだけ渡せば彼らはじきにORを発見するでしょう。

しかし、これにはひとつ大きな落とし穴があります。NOTのときと同じように操作レバーを入力A-Bとすると、ORとは異なる真理値表ができるはずです。なぜなら、シーソーはNOT回路なので、Aが反転されて入力されるからです。

ブリッジの両脇に棒を立てられるようにしてあるのは、この棒をA-Bと見なしてOR回路の真理値を得られるようにするためです。

しかしこれが生徒たちにとって、よい思考訓練になります。生徒たちが、このおかしさに気づいたら、板書で丁寧にその理由を説明し、2本の棒を渡して、再び真理値表を作らせます。

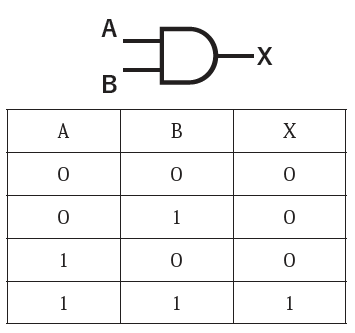
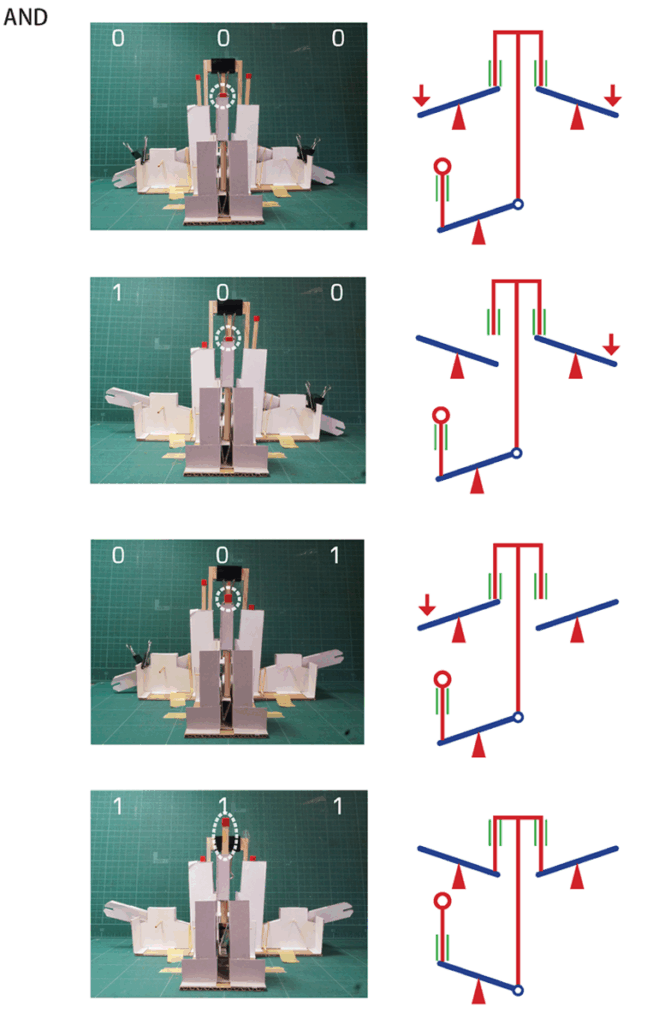
AND

今度は、4人をグループにして取り組ませます。最終的に、3つのシーソーを使用することになります。

シーソーを使ってANDを作るのは、容易なことではありません。彼らがわいわい話し合いながらいろいろ試しても、おそらく解は見つからないでしょう。

最終的には、先生がリンク・バー付きのコの字ブリッジを渡すことで、ようやくANDを見つけるグループが現れます。

そこで先生は、ド・モルガンの法則について簡単に解説します。ド・モルガンの法則に従い、ORの入力と出力の両方を反転することで、ANDが得られたのだということに生徒たちに気づかせます。

この経験を踏まえ、数学的な思考から論理的な仕組みを導くことで、複雑な機構を構築できることが論理装置の特徴であることを説明します。

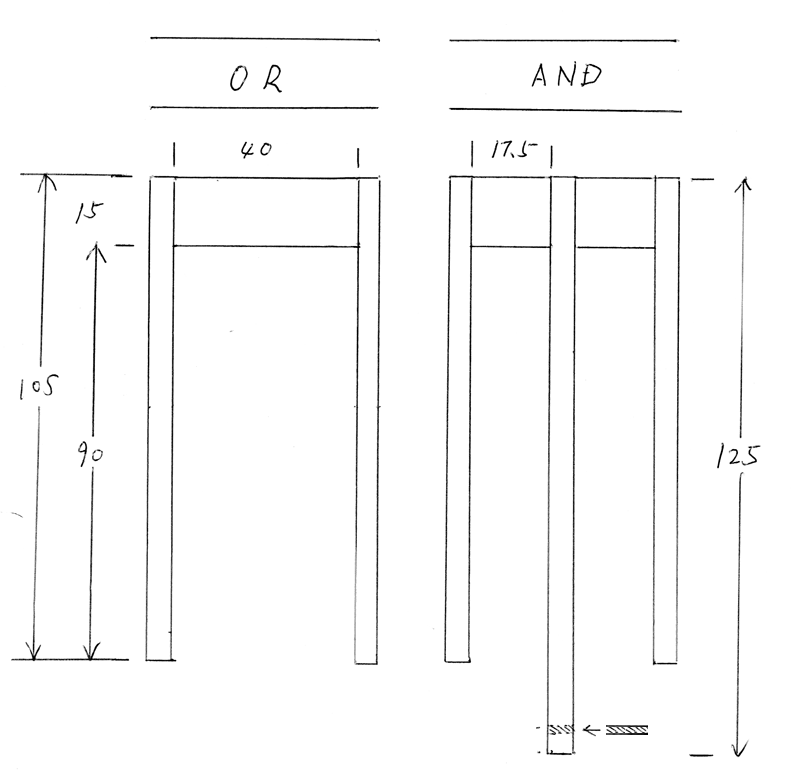
シーソー論理素子の型紙

わたしが設計したシーソー論理素子の展開図、およびパーツの寸法は以下の通りです。

メインユニット

テンプレートを厚紙に印刷して切り抜き、ナイフで折り線に軽く筋を入れて折り曲げ、立体にします。台座は段ボールでよいでしょう。接着は、合成ゴム系接着剤が作業性がよいのでお勧めです。

シーソーの支点と輪ゴムの留木は竹串などを使います。

コの字形ブリッジ

コの字形ブリッジは、15mm x 5mmおよび5mm角の檜材を使いました。ORの入力を確認するロッドも同様です。ANDのリンク軸は竹串を使います。

以下に制作過程の写真を掲載します。