クロックとメモリー
Created by Masashi Satoh | 12/7/2025
はじめに
この記事は、本編の「リレーによる加算機回路製作の詳細」を補強するものです。
コンピュータにおけるメモリー回路の重要性は、言うに及ばないと思います。一方で、クロック回路自体はたんなるオシレーターにすぎません。とはいえ、複雑に絡み合う構成要素が同期して全体の動きを生み出すための重要な仕組みであり、コンピュータに自動マシンとしてのダイナミズムをもたらす要素として、生徒たちが学ぶ価値が高いとわたしは考えています。
この二つの要素を対にして学ぶことにより、コンピューターという無機的な装置のなかに、動と静、変化と保持という対極性の視点を持ち込むことができる点で、この学びはたいへん意義深いものだと思います。たんにクロック信号とメモリー装置の仕組みを学ぶだけに終わらず、コンピュータの学び全体を生き生きとした生命を吹き込むようなイメージを生徒たちに提供できるからです。
そして、何よりも、すでに製作したバッファー回路、NOT回路に帰還をかけるだけという、とてもシンプルな実験でこれらふたつの仕組みの本質を理解できる点でも優れた学びと言えるでしょう。
負帰還回路とクロック
まず、黒板にNOT回路を描きます。そして真理値表をつくり、NOT回路の性質をおさらいします。
その上で、生徒に次のように言います。
「このNOT回路の出力を入力に戻してやると、何が起こるだろうか?」
そして、黒板の上の真理値表で思考実験を行います。
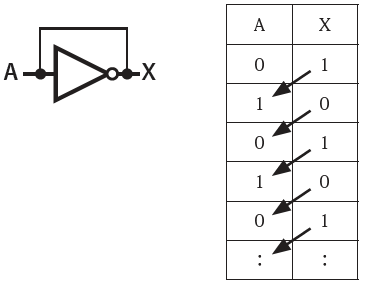
「入力Aの初期値が0だとすると出力Xは1、それを入力に戻してAが1になるとXは0となる。それを入力に戻してAが0となるとXは1となる。それが延々と繰り返されて、Xは0と1を行ったり来たりするはずだね。」
「では、実際にリレーのNOT回路でこの回路をつくってみよう。」
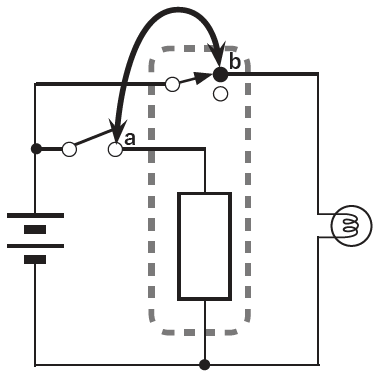
ワークベンチを使って、まずはNOT回路を作ります。そして、真理値表をつくり、動作確認を行います。
次に行うことは、NOT論理の入力と出力が、現実の装置のどこに当たるのかを確認することです。リレーのコイルL端子が入力に当たり、LEDとつながるNC端子が出力に当たるわけです。
この確認ができたら、スイッチAの目玉クリップを外してから、実際に配線してみます。すると、あちらこちらで、ビーッという音とともに小さな歓声が起こるはずです。
少し様子を見守ってから、生徒たちに何が起こっているのかをよく観察するように言います。すると、だいたい次のような答えが返ってくるでしょう。
- リレーが震えて音が出ている。
- リレーのスイッチ部分が高速に振動しているようだ。
その言葉を引き取って、黒板の上のリレーのスケッチ(これはあらかじめ描いておきます)を使って起こっていることを説明し、それが真理値表のXの変化の具体的な表現であることを確認します。これはそれほど難しい作業ではありません。その上でさらに確認します。
「この黒板のとおりだとすると、LEDもついたり消えたりしているんじゃないかな?」
生徒たちは、そうかもしれないという顔をしますが、観察の上では、LEDが点滅しているようには見えません。
そこで、棒の先にLEDを取り付けたものを取り出してみせ、それを生徒の回路に接続します。そして、回路を発振させてから、棒を振ってみせます。すると、確かにLEDの軌跡が点滅して見えるはずです。

人間の目には残像があるため、LEDが光り続けているように見えていたのです。
生徒たちのこの体験を踏まえた上で、これがコンピュータに動きを与えるクロックという信号に使われていることを伝えます。

コンピュータはたくさんの仕組みが組み合わさって複雑な計算を行うので、それらの仕組みがタイミングを合わせられるように、クロックが号令をかける役割をもっているのだと説明します。カッターボートの漕ぎ手が、操舵手の号令にあわせて漕がないとうまく進まないのと似ています。
「はい、つぎ! はい、つぎ!」
身振り手振りで、コンピュータの動作がリズミカルに進行していく様子を生徒たちがイメージできるようにしましょう。そして、このクロック信号がコンピュータに動きをもたらすものであることを印象づけましょう。このイメージができていることが、後のシーケンサーの実験に生きてくるのです。
LEDの点滅を確認するもうひとつの方法は、負帰還回路の遅延をもっと大きくすることです。ワークベンチにリレーが3つありますから、最初のひとつでNOTをつくり、残り2つをBufferにしてカスケード接続します。この3つのリレーで帰還ループをつくると、リレーがパタパタと動き、LEDが点滅するのを観察できます。
ただし、このやり方は複雑さが増して、やや焦点がぼけるので先に述べた方法をわたしはお勧めします。
正帰還とメモリー回路
では、バッファー回路で帰還をかけると、何が起こるでしょうか?
先ほどと同様に、まずは黒板上で思考実験をします。
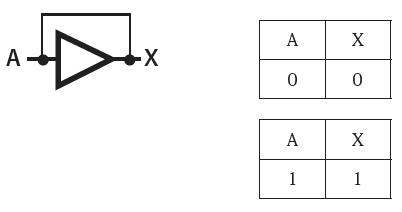
入力Aの初期値が0であれば出力Xは0。それを入力に戻しても、出力Xは不変です。Aの初期値が1の場合も同様です。
こんなものが何の役に立つのでしょうか?
ここで、これがメモリー、すなわち情報を保持する働きとして用いられているのだと話します。詳しく話す必要はありません。すぐに実験に取りかかりましょう。
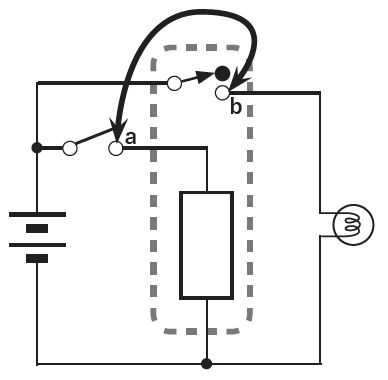
すでにワークベンチに組まれているNOT回路の配線をひとつ入れ替えるだけでBuffer回路になります。そして、ここでも真理値表を作成し、Buffer回路として機能していることを確認します。
スイッチAの目玉クリップを外して、出力と入力をつなぎます。先ほどの実験と手順は同じです。
さあ、ここでスイッチAをONにしてみましょう。LEDが点灯します。さらにスイッチをOFFにします。つまり、目玉クリップを外します。
ここで異変に気づいた生徒が何名かは声を上げるはずです。何が起こったのでしょうか?
スイッチを外してもLEDが消えないのです。
教師は生徒のその驚きの感情を的確にとらえて、これが情報を保持したということだと説明するのです。たったこれだけで、生徒たちはメモリーとはいかなる装置であるのかを、体験的に理解します。
先生に余力があれば、あらかじめワークベンチにデータ書き込みスイッチを追加したメモリー装置を組んでおき、その動作をデモンストレーションすれば、さらに効果的です。(以下のコラム参照)
生徒たちがメモリーとはいかなる装置であるかについて深く納得したところで、帰還の正負によって、動と静、動きと保持という対極の働きが生み出されることに教師は注意を向けます。
全体の授業の流れの中で、適当な場面を捉えて、このようなメモリーが、ENIACでは640個(80Byte)使用されていたのが、2025年の現在では、家庭にある標準的なPCでさえ80億個も内蔵していることを話します。それを可能にしたのは、髪の毛ほどの幅に1,000本の線を刻印することができるほど微細な加工ができるフォトレジスト技術なのです。
この授業以降、帰還をかけたバッファー回路の図を示すことで、生徒たちにメモリー回路の働きを想起させることができるようになります。
データ書き込みスイッチを追加したメモリー装置の回路図を以下に示します。なお、この回路はリレー特有の大きな遅延を利用しているので、半導体のロジック素子では動作しないと思います。
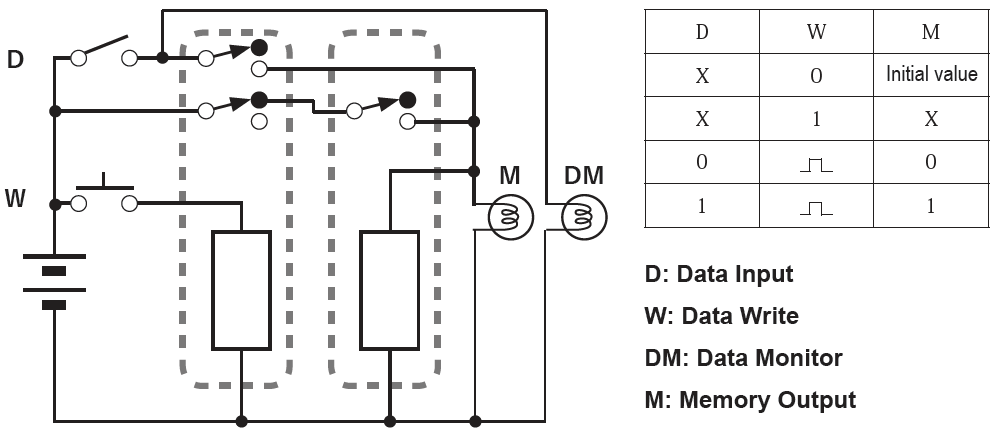
おわりに
すでに触れたとおり、人間の思考を現象に押しつけていくようなある種エゴイスティックなコンピュータ技術についての学びにおいて、帰還の極性に応じて生じる現象と向き合うことのできるこのセクションは、旅の途中でであう清冽な湧き水のように愛すべき学びです。
こうして、生徒たちは、コンピュータを動かす重要なふたつの要素、クロックとメモリーを体験的に学ぶことができます。
クロックの学びは、ダイナミックなコンピュータの動きをイメージすることに役立つとともに、コンピュータの計算速度を規定する要素として、現代の猛烈な処理性能をイメージするためにも役立ちます。
加算機とシーケンサーの接続実験では、このイメージが大いに活躍するでしょう。
メモリーの学びも同様です。このような具体的な体験があるのとないのとでは、生徒たちのコンピュータの理解は大きく変わってくるものと思います。
これらの学びは、リレーによるAND回路、OR回路の実装の学びの後、加算機の学びに入る前に、電信の実験とセットで行います。負帰還による発振回路は、電信装置を制作する異実習の際にブザーの代用として活用するとよいでしょう。
リレーのNOT回路に帰還をかけると発振するのは、リレーの場合、入力の変化に出力が反応する速度が非常に遅いためです。この遅延が小さくなればなるほど、発振周波数が上がっていきますが、最後には振幅が小さくなり反転増幅器として動作するようになります。
小さな動きに対して敏感に反応するという点で、増幅器も発振器同様の動的な性質を変わらず保持していると言えます。
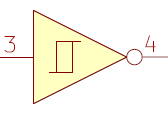
正帰還の特性を使った仕組みには、チャタリング除去などに使われるヒステリシス回路があります。一度、モードが切り替わると、容易にはモードを変化させないという保持作用を利用した回路と言えます。
磁気記憶装置なども含めて、すべてのメモリーはこのヒステリシスな性質を利用して状態を保持しているのです。
負帰還の動きはヤジロベエのようなイメージで捉えるとよいでしょう。正帰還の動きは四角形の積み木のようなイメージで捉えるとわかりやすいと思います。

- ヴァルドルフ/シュタイナー教育におけるICTカリキュラムの骨格を形づくる
- The History of Computers(Currently being produced)
- リレーによる加算機回路製作の詳細
- シーソーによる論理素子
- クロックとメモリー
- リレーの起源と電信装置
- シーケンサーについて
- About the Battery Checker(Currently being produced)
- インターネット
- データモデルの学び
- Learning Programming and Application Usage Experience(Currently being produced)
- Human Dignity and Freedom in an ICT-Driven Society(Currently being produced)