リレーによる加算機回路製作の詳細

Created by Masashi Satoh | 11/04/2025

はじめに

本記事では、「ヴァルドルフ／シュタイナー教育におけるICTカリキュラムの骨格を形づくる」に示した授業プランの「すでに広く実践されているリレーを用いた多桁の加算機の製作」について詳しく解説します。

多桁の加算機製作に取り組むこの授業は、コンピュータ技術とインターネットの概要を理解することを目的として、2013年より毎年、横浜シュタイナー学園の9年生の終わりに私が実施している2週間10回のメインレッスンです。

ここではコンピュータがいかなる原理で動作しているかを、生徒たちが自分自身の思考の力と直観によって把握するための最良の教材として、リレーによる加算機回路とそれに接続することで自動計算を可能にするシーケンサーについて紹介します。

この授業のためにわたしは8 x 3bitの簡単なシーケンサーを設計しました。これまでの授業実践を通じて、これが、メモリーを説明するための教材としても、パンチカードを想起させる教材としても、表示装置の説明教材等々として応用可能な万能教材であることを確認しています。

この装置のデモ動画もこの資料のなかでご覧いただけます。

この授業プランがどのように成立したのかについては、以下の文書に書いていますので、そちらをご覧ください。

授業の流れ

このひとまとまりの授業は、ICT環境があふれている日本社会の状況から、生徒の関心が早くそちらに向かいがちであることや、10年生以降からPCに触れる可能性があることへの対応として9年生で実施しています。

丁寧に授業を進めることで、9年生でも無理のない学びを実現できたが、年齢としてはやや早すぎる内容だとわたしは感じています。その国や地域の状況が許すなら、PCへの接触は先延ばしにしてこの授業を10年生以降に実施するとよいでしょう。

わたしが実施している授業の流れは、以下の通りです。

日常生活と論理操作

私たちは、あらゆるディジタルコンピュータが、ANDとNOT、またはORとNOTというたった二つの論理によって構築されていることを学んでいくわけですが、そのような論理を私たちが日常のなかで用いていることをその学びの出発点にします。

旅行に出かけるための条件をAND結合していたり、今晩のおかずの選択肢をOR結合したり、そのような事例から始めて、そような論理が機械のなかでも応用されている事例へと導きます。

たとえば、エレベーターが昇降する際に、扉が閉じている、重量がオーバーしていないこと、地震などの揺れを検出していないことなどの条件をAND結合することで、安全機構が正しく働いていることを図示するとよいでしょう。その際、○と×による真理値表に整理します。

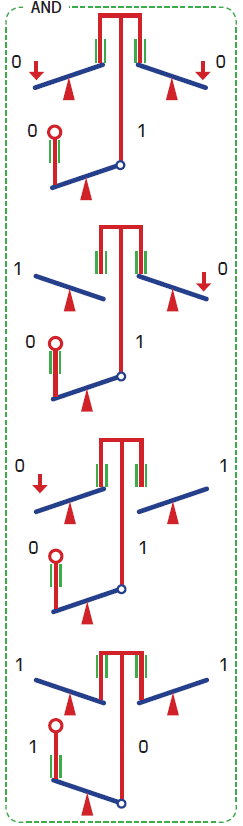
では、バスの次の停留所で降りたいときに運転手に知らせるためのブザーボタンの回路にこのAND論理を使ったらどうなるでしょうか？ そんなユーモアを用いると、生徒たちは論理の世界と自らの日常経験を生き生きと結びつけることができるでしょう。もちろん、この回路はOR論理を用いて作らねばなりません。

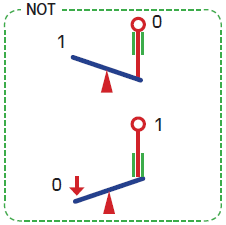
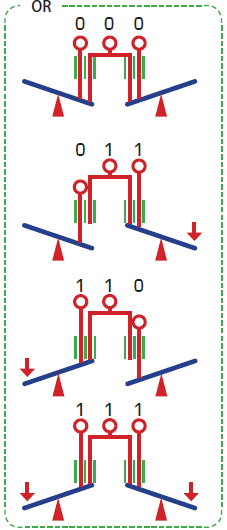
このような導入の後、NOT論理を日常のなかに探すときに、私はシーソーを例に挙げています。そして、実際にシーソーを使って、NOT、OR、ANDの仕組みを試しています。

この実習により、論理が電気の仕組みを使わなくても実装可能であることを示すとともに、論理の実装を可視化し、その動きを実感することが可能となります。

また、シーソーによってORを作ることは容易ですが、ANDを作ることはたいへん難しいことを体験させ、その上で、ド・モルガンの法則によって解が得られることに導くことで、観察から導かれて発展してきた蒸気機関などの技術とはコンピュータは逆方向の方向性をもつ技術であることに言及するとよいでしょう。

厚紙を使ったシーソー論理の詳細は以下のページで説明しています。

リレーの観察と配線の練習

シーソーによる論理装置をひととおり体験した後、リレーと呼ばれる電磁スイッチを取り上げます。これから取り組む多桁の加算機は、これを使って製作します。前提として、生徒たちが電磁気学のエポックを終了しており、回路と電磁石についての知識をもっていることが必要です。

最初にリレーをひとりずつ配り、観察します。

用意するリレーは、底面サイズが28mm x 21.5mmの透明なケースに入った定格電圧DC12Vで2回路の制御用リレーが適当です。それは以下のような理由によります。

• ケースが透明なので、仕組みや動作を目視で観察できる
• 比較的大きな動作音がするので、動いている実感が伝わる。とくに自動計算させた際の感動が大きく、計算とともに複雑なリズムを刻むので、コンピュータミュージックの説明にも使える。
• コイル端子の幅が006Pタイプの9V電池の端子と同じ間隔なので、電池を直接接触させて動作を観察することができるので好都合
• 006Pタイプの9Vアルカリ電池で全加算機程度の回路を駆動できるのは便利
• 比較的安価で入手性が良好

回路図と実配線の関係性に習熟させる

この時点で、生徒は回路図と実配線の関係性を理解していませんから、まずはそれに慣れるための時間を設けます。ここを丁寧に進めることで、作業内容についての理解も容易になり、授業全体がスムーズに進むようになります。

わたしは次のような手順でこれを進めています。

• バッファ論理の回路図と部品の図（写真）を並べたワークシートを用意し、手描きで結線を配線させる。その際、電池の＋極から順に回路を追っていくことを徹底させる。
• 出来上がった結線図を見ながら、実配線する。
• 完成したら、真理値表を作成し、設計通りの動作をしているかどうか確認する。
• NOの結線をNCにつなぎ直してみる。NOT回路になっていることを検証する。

以上の実習は、個別の部品を用意すれば可能なので、生徒一人ひとり、全員が経験できるようにすることが望まれます。

ワークベンチを使った実習

空中配線による実習で、回路図と実際の配線の関係性を理解できたら、以後はワークベンチを使って作業を進めます。わたしが作ったのは、リレーを3台搭載し、2つのスイッチと2つの抵抗内蔵型LEDランプ（定格電圧12V）を備えたワークベンチです。

最終的にワークベンチ上で作成する半加算機はリレー2個で構成しますが、万一、リレーが故障したり、配線が取れたりした場合のスペアとして3個のリレーを載せています。また、2台の半加算機を全加算機として構成する際に、キャリーを合成するためのOR回路用にこのリレーを用いています（後述）。

ワークベンチは、リレーのすべての端子をラッピングワイヤで真鍮製のネジ釘に引き出しただけの単純なものです。ただし、ネジ釘を2本立てて構成するスイッチの片側は電池のプラス側に配線済みとし、LEDのカソード側とリレーのコイルの片側は電池のマイナス側に配線済みにして、生徒の配線作業量を減らせるようにしてあります。

また、通常の実習には006Pタイプの電池を用いますが、多桁の加算機を組み上げる最終段階ではすべての全加算機をデイジーチェーン式につなぎあわせて安定化電源に接続するので、雄雌一対の電源コネクタを取り付けています。わたしは、HDD用のペリフェラル・コネクタ延長ケーブルを半分に切って使っています。

リレーのコイルには必ずサージ電圧抑制用のダイオード（1N4007等）を取り付けて下さい。これを付けないと、自動計算用のシーケンサー回路を接続した際に、装置が誤動作します。また、希にいる電気に敏感な子どものための対策でもあります。

このネジ釘にワニ口クリップ付きのケーブルを使って回路を配線していきます。ワニ口クリップの作業は、半田付けよりは簡単に作業でき、バナナプラグよりも集中力を要する点で、この学びに適しているとわたしは感じています。

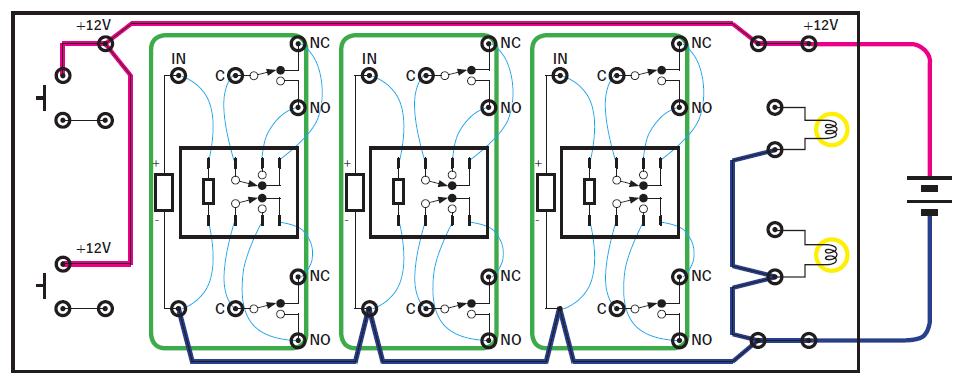
AND回路とOR回路

さて、次に行うべきことは、コンピュータを構成する基本論理であるAND回路とOR回路をリレーで作ることです。

まずその前に、黒板の上に電池と電球を繋いだ閉回路を描いて見せ、ここに2つのスイッチをどのように配置したらANDができるかを生徒に考えさせます。これは比較的容易に見つかるはずです。OR回路はやや難易度が上がりますが、それでも発見する生徒はいるでしょう。そしてこれらが、直列つなぎと並列つなぎの違いであることに気づかせます。

これらのスイッチを電磁石によって操作できるようにした仕組み（リレー）を用いて、これから様々な回路を作っていくのだと生徒たちが理解できたなら、実習に取りかかります。

リレーを用いたAND回路、OR回路の回路図を黒板に描き、その回路図通りにワークベンチ上にこれらの回路を作っていきます。その際、次のことに留意して先生は生徒を指導する必要があります。

• 最初に、ワークベンチ上ですでに結線済みの配線がどれであるのかを確認します。
• スイッチ、リレーの各端子、LED、電源がワークベンチにどのように配置されているかを確認します。
• 電池のプラス極から出発して回路の流れを追いながらマイナス極に向かって結線していきます。
• 最後に電池を接続し、スイッチのすべての組み合わせを試し、電球のON/OFFとの関係を真理値表にします。（もちろん。）

以上で、生徒はリレーを用いて、AND、OR、NOT、Bufferのすべての回路を作り上げることができました。これだけでも、彼らには楽しく、また誇らしい体験です。

正帰還と負帰還、メモリーとクロック

私たちはここからすぐに計算機の製作に取りかかることはしません。その前に、メモリーの仕組み、クロックパルスを発生させる仕組みを実習によって学んでおきます。これがコンピュータ装置の全体像を生き生きと理解するための布石となります。

これらの理解には、対極性の視点がたいへん役に立ちます。負のフィードバックと正のフィードバックを用いるのです。

その詳細は、以下の独立したセクションで説明しています。

電信の仕組みー伝送の基礎

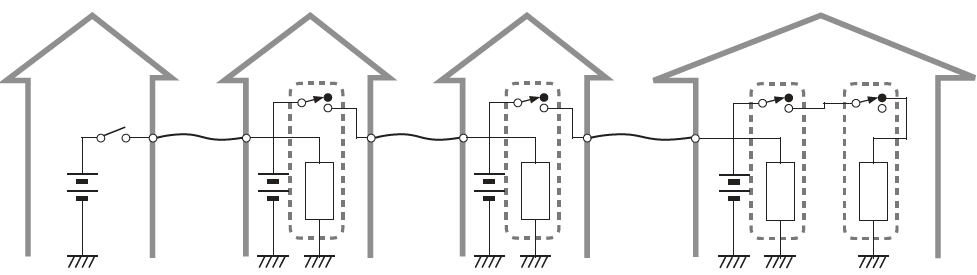
ここでもうひとつ重要なテーマを挿入します。電気的な伝送技術の基礎である電信技術を説明し、実際に実験するのです。

「なぜ電磁スイッチと呼ぶべき装置がリレーと呼ばれるようになったのか」という歴史的経緯から導入するとよいでしょう。

SOSなどよく知られたモールス符号を取り上げ、スイッチのON/OFF時間の長短で遠地に情報を送る装置である電信技術を説明します。発信元にはキースイッチがあり、そのスイッチから送られる電力が電線を通して送信先に伝わり、ブザーを鳴らします。

ところが、電線にはわずかながら抵抗があるため、伝送距離が長くなると熱になって失われる電力が大きくなり、受信地点の電圧が小さくなるという問題がありました。そこで中継地点に電磁スイッチと電源を置き、飛脚がリレーしていくように、電力を増幅して送信先まで届くようにしたためリレーという呼び名がついたわけです。

この話の際に、アースを使って帰路の電線を節約できることも話題にするとよいでしょう。ルドルフ・シュタイナーの言葉を借りれば、「地球は電気を通す」のです。

このような説明の後、実際にこの仕組みを作ってみます。

適当な数の中継基地のワークベンチ上にバッファ回路を作り、長めのコードを用意して基地間を繋ぎます。最後の装置には、前項で作成した負帰還回路を追加します。これがブザーとなります。

いちばん先頭の中継所には、シーソーロジック回路にゼムクリップなどで接点を設けたキースイッチを接続します。

こうして完成した電信システムは教室の端から端まで確実にスイッチの操作を伝え、末端のブザーを鳴らす様子は壮観であり、生徒たちはたいへん感動します。

後のインターネット技術の学びの際には、電気のON/OFFで情報を伝える電信の仕組みはインターネットにも変わらず使われていることを話します。

このようなイメージを生徒がもつことが重要なのです。

リレーを用いた加算回路の構築

さて、ここからようやく私たちは加算機に取り組みます。

まず、わたしたちがなぜ足し算の装置を作るのか、その理由を生徒にきちんと説明します。コンピュータの減算は2の補数を加算することで実現しており、乗算も除算も数値をシフトして加減算するだけなのです。そのような理由から、加算の仕組みを知ることが重要となります。

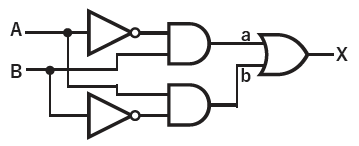
そのようにして目標を明確に定めた上で、黒板に二進数の足し算を例示し、1桁目の計算を論理回路で実現する方法を考えます。その際、桁上がりは考えず、1桁目の数値のパターンだけに注目します。そして、このパターンがOR論理とよく似ていることを生徒に気づかせます。1＋1の結果のみが求めているパターンと異なっているわけです。

世界中の科学者や技術者が、単純な加算機の仕組みを探しましたが見つかりませんでした。仕方がないので、彼らは、入力が1＋1のときだけ、OR回路の出力を強制的にゼロにする方法がないか考えました。

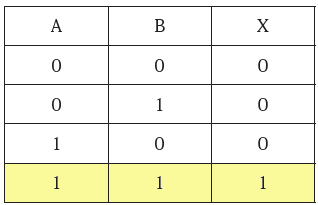
まずやらなくてはならないのは、入力が1＋1であることを検出することです。これがAND回路で実現できることは、容易に見つけられます。

次にな為すべきは、AND回路の出力が1になったときに、OR回路の出力を強制的に0にする仕組みを探すことです。

ここは、ゲートという考え方を理解するのにふさわしい場面です。わたしは、次のようなよく知られた絵を生徒に見せています。（意外なことに、生徒たちはこの絵に夢中になります！）

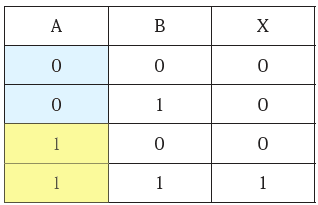
人間は、同じ図柄から視点を変えることで異なる意味を見出す能力を有しているわけです。同じ目でAND回路の真理値表を眺めてみましょう。

すると我々はそこに開いたり閉じたりする門を見出します。ANDの入力の片側が1のとき、この門は開き、もう一方の入力をそのまま出口に素通りさせます。しかし制御側が0になると門は閉まり、出口は0に固定されるのです。

このような見立てによって、AND回路はゲートという性格をも与えられるようになりました。わたしたちも、我らの加算機にこの考え方を用いようではありませんか。

この門は制御信号が0のときに閉じるので、先ほどの1＋1検出用のANDの出力を反転させればそれがこの信号として使えます。

こうして足し算の1桁目が実現できました。

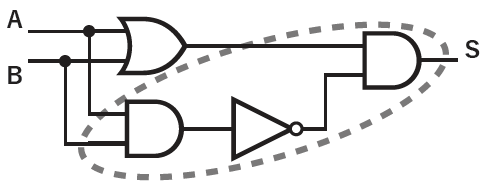
ここまでできれば、桁上がりの仕組みも簡単です。桁上がりは1＋1のときに起きるのですから、AND回路の出力がまさにそれです。それはすでに実装済みでした。

これで明らかになるのは、この標準的なコンピュータの加算回路は、実際には足し算などしていないということです。ここで行われていることは、足し算のパターンをパッチワークで作っているにすぎません。そのことも生徒たちと一緒に確認しておきましょう。

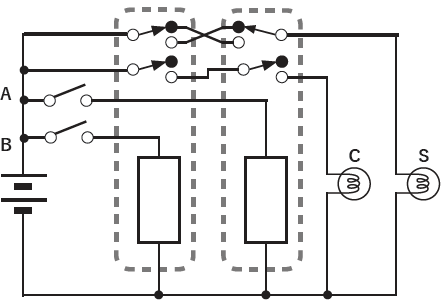
リレーの節約：階段の電灯方式XOR回路

ここまでで、私たちは半加算機の仕組みを理解しました。これから、それをリレーによって実装していくわけですが、これだけでもかなり大がかりな装置になることが予想できるのではないでしょうか。単純に考えて、ふたつのAND回路に4つ、OR回路に2つ、NOT回路に1つのリレーが必要で、この装置には総計7つのリレーが必要になります。

使用するリレーにはスイッチが2組入っているので、入力を共有しているORとANDのセットは2個のリレーで作ることができますが、それでも5個のリレーが必要になります。

わたしたちのワークベンチには3台のリレーしか載っていませんから、なんとしてももっと節約したいところです。

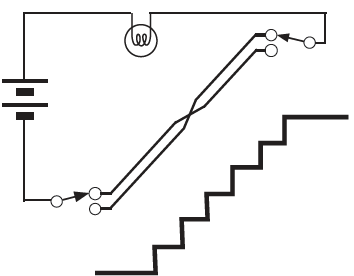
そこで、生徒に次のような話をします。「君たちの家には階段があるかい？ 階段の電灯は、下の階と上の階にひとつずつあるスイッチでON/OFFできるようになっている。このスイッチA、Bの状態と電灯の関係について真理値表を作ってみよう。」

そして、階段の電灯の回路図を示しながら、真理値表を作成します。真理値表を整理し直すと、私たちはそこに足し算のパターンが浮かび上がることを発見するでしょう。

この回路なら、2個のリレーで加算機を構築することが可能です。同じリレーの余ったスイッチでAND回路も構築できるので、2個のリレーで半加算器をつくることができるわけです。この仕組みを使わない手はありません！

グループによる作業

この方針に沿って作業を進めていくために、グループ作業について考えておきたいと思います。

非常に少人数のクラスの場合を除いて、ワークベンチを用いた作業は2人ペアで行うとよいでしょう。お互いに助け合って作業を行い、真理値表を作る際には、操作と読み上げを行う担当と結果を書き留める担当のように分担して進めることが可能です。

最終的には全加算機を作るので、2つのペアを一塊の島にして4人のグループで作業を進めるのが理想的です。

最初にシーソー回路を作るときからこのグループを構成して、一貫して作業を進めていきます。シーソーNOTは一人ひとり作成し、それをペア同士で合わせてORを形成し、4人で力を合わせてANDを作るというように。

電信の実験では、ひとつの島あたりひとつの中継所をつくり、長い線で島と島をつないでいきます。

この島グループは、資料を渡してそれについて考察したり、話し合ったりするのにもよく機能します。

全加算機から多桁の加算機へ

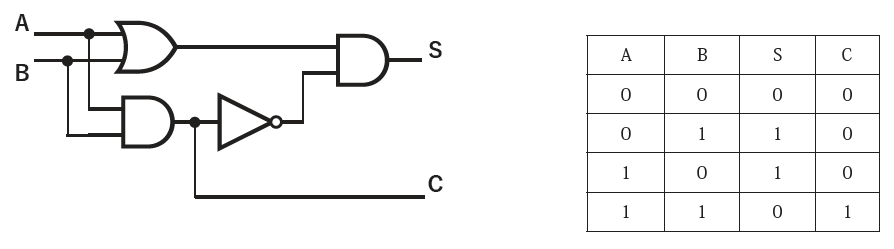
全加算機の仕組みを以下に示します。

半加算機から多桁の加算機に至る手順を以下に示します。

論理の理解から始まり、リレーの観察と配線の練習、リレーを使ったいくつもの実験を重ねてきて、作業に十分に慣れた生徒たちであれば、上記の作業を3日間で行うことができます。

最後の多桁の加算機の検証を行う桁数は、3桁が適当です。これだと64通りのパターンとなり、ちょうどよい作業量です。

できれば、以下のような操作パネルを用意するとよいでしょう。

2名の生徒を指名して、ひとりが捜査担当、もうひとりが読み上げ担当になり、クラスの残りは予め配布した記録用紙に結果を書き取りながら、暗算で検証していきます。誤りが見つかれば、もちろん声を上げてもらい、結線を点検します。

スイッチBが0-0-0の状態からスイッチAのすべての組み合わせ8通りをセットし、その度にランプの値を0/1で読み上げます。

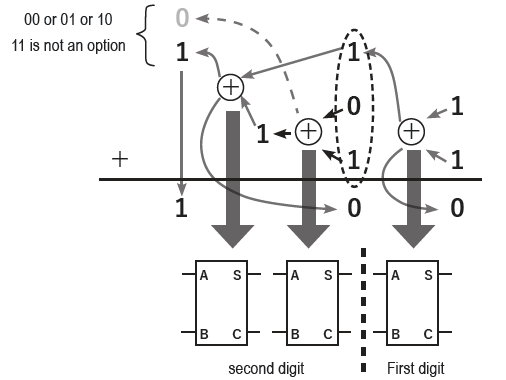
これを3ブロックほど作業して、結果が間違っていないことを確認した後、いよいよここでシーケンサーを接続します。

計算機からコンピュータへ

手作業での計算機の検証は楽しい体験です。しかしこれを一日中やらなければならないとしたらどうでしょうか？ 先人たちは、この作業から人間を解放するためにコンピュータを開発してきたのです。

このような話をした後に、3 x 8bitのシーケンサーを生徒に見せて、その動作を説明します。

やや複雑ですが、実際に実演しながら説明すれば生徒たちはすぐに理解します。

生徒たちが納得したら、この装置に0から7までの二進数のパターンをセットし、加算機のスイッチAに接続します。その際、加算機のスイッチはすべてOFFにしておきます。

シーケンサーの二進データをステップ操作で加算機に送り込み、加算機が動作することを確認した後、残った検証パターンをこの方法ですべて確認し、64パターンの真理値表を完成させます。

これだけでも、かなり作業がスムーズに進んだと皆が思うでしょう。しかしまだこれだけでは自動マシーンとは言えません。

そう言いながら、先生はシーケンサーのクロック回路のスイッチを入れます。

生徒たちからは驚きの声があがるはずです。皆で作り上げたモンスターマシーンが、生命を吹き込まれたように音を立てて動き始めたのです。

そう、これこそが、バベッジやその追随者たちが作ろうとした自動マシーンなのです。

この感覚的な体験が、この学習の要となると私は考えています。彼らにとって、コンピュータはもはやブラックボックスではなくなったのです。

このシーケンサーは、クロックスピードをボリュームで制御できるように作ってあります。クロックを非常に遅くした状態で、「バベッジの解析機関はこのくらいのスピードだろう」と伝え、次第にスピードを上げていきながら「Z1はこれくらい」、「ENIACはこれくらいの感じだね。（実際はもっと早かったけれど。）」というようなやりとりをすれば、クロックスピードとコンピュータの処理速度の関係が体感できます。

その際、シーケンサーのランプの並びが、バベッジの解析機関のパンチカードと同じ働きをするものであることも、しっかり生徒たちと確認しておきましょう。

コンピュータシステムの全体像

この先のデータモデルの学びにつなげるために、コンピュータの仕組みをさらに掘り下げます。ここからはすべて黒板上で講義を進めていきます。

ここで大事なのは、バベッジやコンラート・ツーゼが構想したパンチカードのイメージから離れないことです。ノイマン型のコンピュータについて触れる必要はありません。

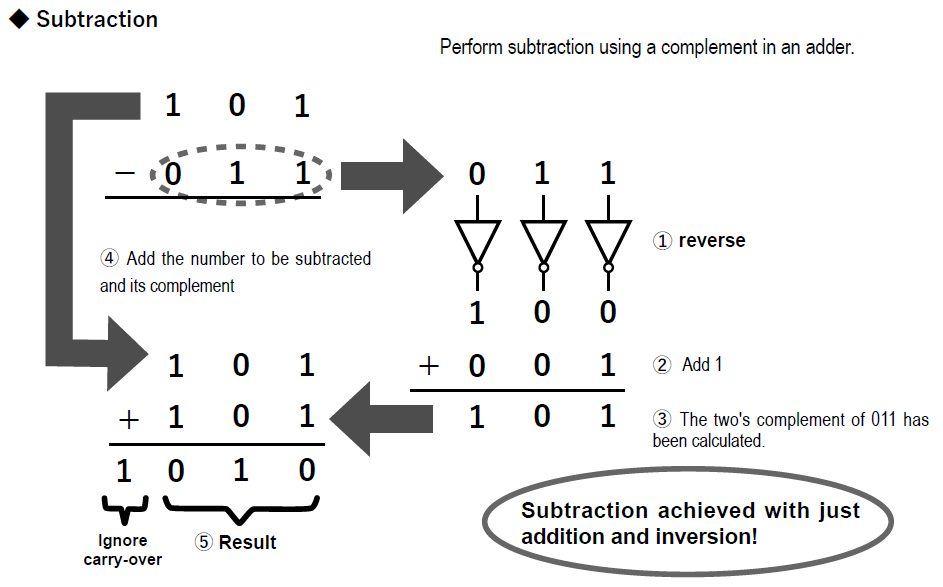
まず、二の補数を使って加算機から減算機が作れることを解説します。さらに、シフト操作と加算によって乗算ができ、シフト操作と減算で除算ができることを話します。このようにして、簡単に四則演算が可能となります。

この知識に基づいて、論理演算装置ALUを取り上げます。黒板に大きく印象的なV字型の論理演算装置の記号を描きます。

その上で、この装置が、バイキング方式のレストランのように、あらゆる演算や論理処理のメニューをあらかじめ用意してあり、客のリクエスト(F)に応じて選べるようになっていることを説明します。

ここで教師は直前のシーケンサーをつないだ計算では、加算機の数値入力にメモリー上に設定した数値を次々に送り込むことで自動計算を行ったことを確認し、生徒に次の問いを出します。では、もしもシーケンサーに演算処理の手順を設定して、ALUのFunction端子に送り込んだらどうなるでしょうか？

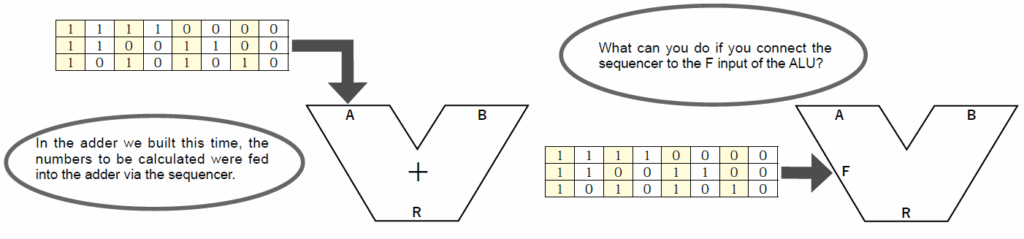
そう、このようにしてコンピュータは、計算や論理操作などの手順を次々に送り込んで、一連の処理を行っているのです。

このイメージが生徒たちと共有した後に、番地が振られたメモリー素子がコンピュータの内側に並べられていることを伝えます。ALUはメモリーからデータを引き出して処理し、結果を戻すことを繰り返して複雑な処理を行うのです。

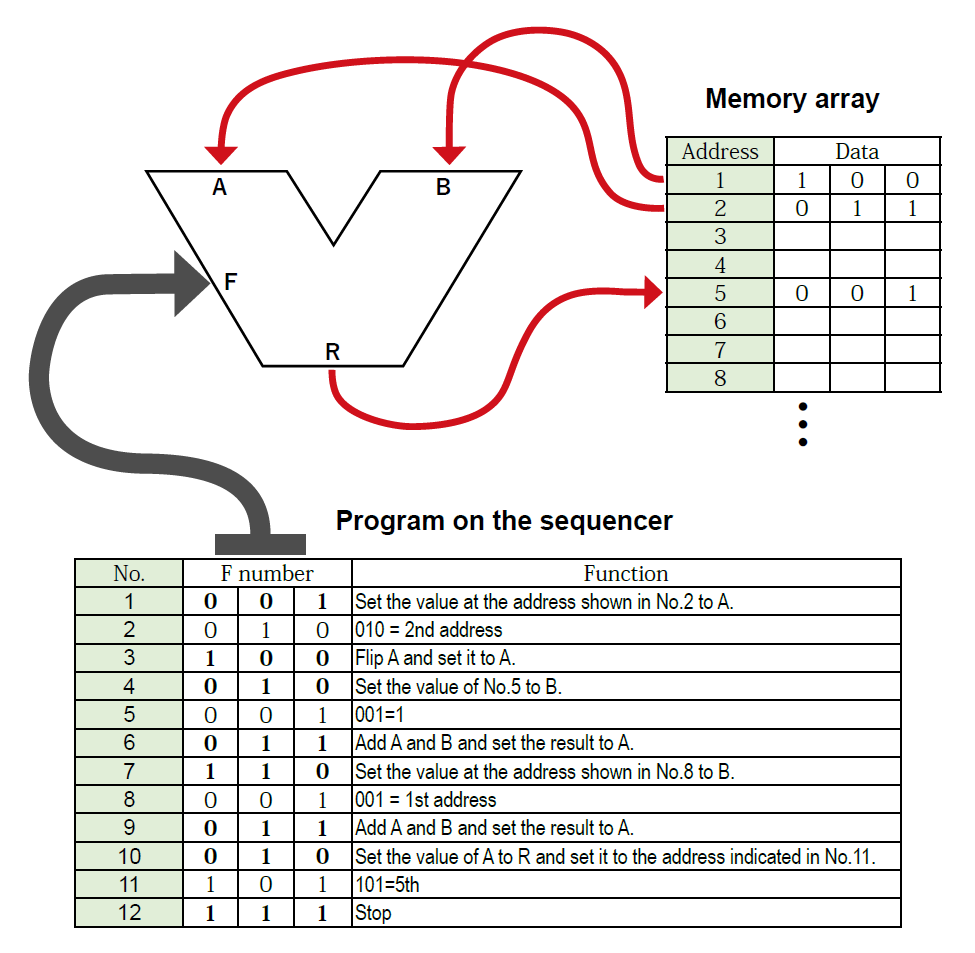
わたしは、二の補数を使った減算処理のプログラムを例に説明しています。たったこれだけの処理に、たくさんのステップのプログラムが必要であることに生徒は驚きます。

実際、このような面倒な手続きを山のように積み重ねなければ、コンピュータは人間が意図する結果を出すことができません。コンピュータが非常に高速にそれを行うために、それが人間に意識されることがないだけなのです。そして、そんな面倒な手続きも、一度つくってしまえば、使いまわしができるので、いちいち作り直す必要がないのです。

このように、高速化、メモリーの大容量化、そしてプログラムの使いまわしの技術の進歩によって、コンピュータは発展してきたのです。

情報処理の基礎

締めくくりに、コンピュータ内部で様々な情報をどのように扱っているかを、簡単に説明します。

数値が扱えることは、すでに理解しました。では、文字をコンピュータはどのようにして扱うのでしょうか。

つまるところ、コンピュータは数値しか扱えません。もっと言えば、人間が数値として意味づけしたパターンを扱っているだけです。数値という概念を、特定のパターンに紐づけているのは人間なのです。

文字も同様に、人間がある文字を特定の数値と1対1で対応付けておき、その関係性を念頭に置きながら、文字処理の結果を導けるように数値情報を操作するプログラムを用意するのです。

生徒にこのような説明をする必要はありませんが、教師がこのことを理解していることは重要です。

生徒には、たんに、数字と文字の対応表を示します。単純なものがいいでしょう。

重要なのは、文字処理の例示に何を選ぶかです。いちばんいいのは検索処理です。単純な検索処理の例を示して、説明します。

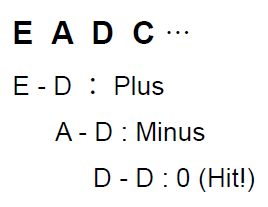
たとえば”EADC”という文字列から”D”を探すとします。まず、最初の文字、”E”を取り出します。もちろんメモリ上には、”E”に対応する数値が置かれているので、扱うのは数値です。コンピュータはここで、引き算をします。”E”から”D”を引くのです。

結果が0でなければ、次の文字を調べます。”A”、”D”と調べて、初めて結果が0となります。”D”を発見したわけです。

非常に単純化してはいますが、これこそが検索技術の根本です。検索は引き算で行われている。AIが行っているパターンマッチングでさえ、根本は引き算だ。簡単だ。そんな印象を生徒が持てたなら、それは教育的な成果です。

文字の表示は、シーケンサーの表示器を使って説明します。たんに101のように、パターンをセットして見せれば、すぐに生徒は納得します。コンピュータは文字を表示しているのではなく、その文字に対応する文字形のパターンを、メモリーの上に並べているだけなのだと。

ついでに、ここでクロックをONにすれば、動画の仕組みも説明できてしまいます。一石二鳥です。

カラー表示の仕組みの説明は、RGB画素の拡大写真を見せます。三原色の水彩に親しんだ彼らは、すぐに理解します。

二次元情報の電送の仕組みも、簡単に説明しておくとよいでしょう。

音声情報の量子化も簡単に説明できます。音声は、音響学で学んだ音の振動を電圧の変化に変換し、さらにそれを数値化できることを示します。数値を電圧に逆変換してスピーカーを鳴らせば、その音が再生されます。

最後にI/Oです。

キーボードを例に挙げ、Aのキーを押すと先に説明した”A”に対応する数値が出てくることを説明します。コンピュータの方では、メモリーの列のなかに空き番地を設けておき、その番地にキーボードの出力を配置しておきます。この番地の内容をコンピュータが読みだすと、”A”の値を得ることができるわけです。

出力はその逆です。

以上のように、やや駆け足ではありますが、メインレッスンの一コマで、ほぼコンピュータシステムの全体像を生徒たちに提供できました。

インターネット

10日間の最後の学びでは、インターネットを取り上げます。その詳細は別項にて扱っています。

おわりに

以上の内容を全10回の授業にまとめるのは、慣れないうちはたいへんかもしれません。導入時には、試行錯誤の時間を多めにとって、余裕をもって進めることをお勧めします。逆に、慣れてくると、出張授業などのようにやむを得ない場合、一日2コマで5日間で実施することも可能です。

長年取り組んでみて、この授業プランは、生徒たちが男女関係なく大きな充実感を得ることができる点で、たいへん優れた実践だとわたしは思っています。授業が終わったとき、PCに触れる前にこの学びができて本当によかったと語った生徒もいました。「世界中の人たちがこの授業を体験するべきだ」とノートに書いた生徒もいます。わたしもそう思います。

これからますます発展していくコンピュータ社会のなかで、コンピュータの原点、そして人間存在の原点に触れられるこの授業はますます価値を高めていくだろうと私は確信しています。